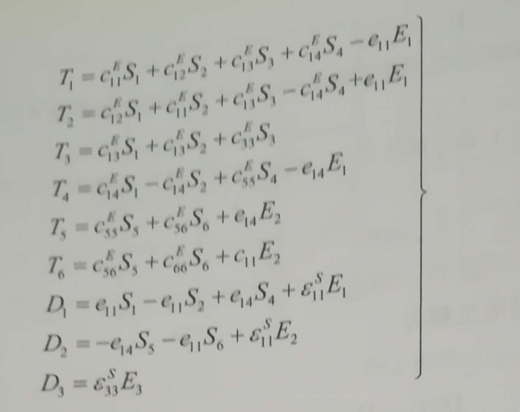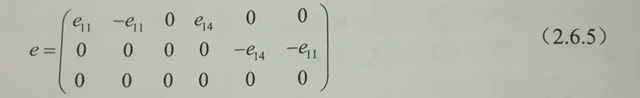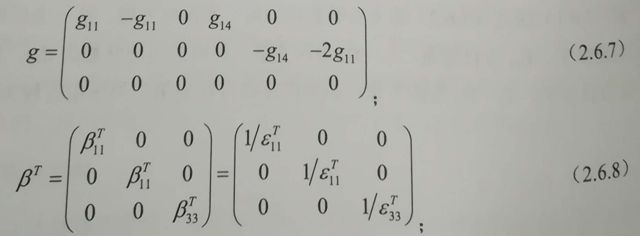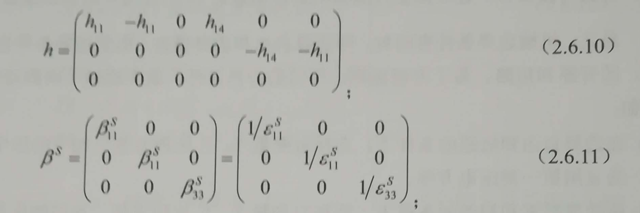石英晶體的壓電方程
大家都知道石英晶體諧振器是具有壓電效應的,因此通電之后才可以振蕩,帶動其他的電子零部件工作。石英晶振的壓電性能是獨一無二的,因此才會成為產品內部最核心最重要的元器件,想要制造一顆完整晶振,計量與測量是必不可少的。
通過前幾節討論,我們知道,晶振介電性質所遵循的電學規律是用介電方程來表達的,介電方程反映了電位移D與電場強度E之間的線性關系。晶體的彈性性質所遵循的力學規律是用彈性方程來表達的。彈性方程反映了應力張量T與應變張量S之間的線性關系。同樣,壓電石英晶體的壓電性質所遵循的機電規律是用壓電方程來表達的,壓電方程反映了D、E、T、S四個量之間的線性關系。
一、壓電方程
石英晶體諧振器是彈性介質,也是電介質,在應力張量T和電場E的分別作用下,
將產生彈性應變和介電電位移,即:
S彈=SET;
D介=εTE;
式中,SE為E=0(或常數)時的彈性柔順常數矩陣;εT為T=0(或常數)時的介電常數矩陣。
無源晶振也是壓電體,在T和E的作用下,將通過正、逆壓電效應產生壓電
應變和壓電電位移,即:
S壓=dtE;
D壓=dT;
所以,音叉晶振的總應變和總電位移為
S=S彈+S壓;
D=D壓+D介;
即:
式(2.6.1)或式(2.6.2)稱為石英晶體的第一類壓電方程。第一類壓電方程的特點是以Tj、Em為自變量,Si、Dn,為因變量,相應的壓電常數為dmj。如果選SJ、Em品為自變量,Ti,Dn,為因變量,相應的壓電方程為第二類壓電方程為:
式中,CEij為E=0(或常數)時的短路彈性常數;εsmn為S=0(或常數)時的介電常數,稱為受夾介電常數,式(2.6.3)也可以寫成矩陣形式,即:
式中,壓電常數矩陣e為:
如果選Tj、Dm為自變量,Si、Em為因變量,則相應的壓電方程為第三類壓電方程:
式中,sD為D=0(或常數)時的彈性柔順常數矩陣,g為壓電常數矩陣:βT為自由介電隔離率矩陣。G和βT的表達式分別為:
如果選Sj、Dm為自變量,Ti、En為因變量,相應的壓電方程為第四類壓電方程:
式中,cD為D=0(或常數)時的彈性剛度常數矩陣;h為壓電常數矩陣;βS為受夾介電隔離率矩陣;h和βS的表達式分別為:
相關技術支持
- Mtron為雷達應用提供的射頻組件與解決方案
- Microchip的JANSPowerMOSFET解鎖太空可靠性新高度
- BomarCrystal專注于表面貼裝(SMD)晶體和振蕩器產品的研發與生產
- Pletronics普銳特MEM產品與傳統石英產品的對比分析
- Murata村田實現1608尺寸車載PoC電感器助力設備實現小型化輕量化
- 引領汽車照明革命Diodes智能48通道LED驅動器的技術突破
- Diodes推出的3.3V四通道混合驅動器能夠確保HDMI2.1信號完整性從而實現高分辨率視頻傳輸
- Taitien利用超低抖動VCXO推動5G及更先進技術的發展
- 利用ECS公司的精確計時解決方案來保障數據中心安全
- ECS這款可靠的定時組件為當前和未來的網絡應用提供了出色的性能


 手機版
手機版